4.2 Polar Cases of Elasticity and Constant Elasticity

There are two extreme cases of elasticity: when elasticity equals zero and when it is infinite. A third case is that of constant unitary elasticity. We will describe each case. Infinite elasticity or perfect elasticity refers to the extreme case where either the quantity demanded (Qd) or supplied (Qs) changes by an infinite amount in response to any change in price at all. In both cases, the supply and the demand curve are horizontal as Figure 4.4 shows. While perfectly elastic supply curves are for the most part unrealistic, goods with readily available inputs and whose production can easily expand will feature highly elastic supply curves. Examples include pizza, bread, books, and pencils. Similarly, perfectly elastic demand is an extreme example. However, luxury goods, items that take a large share of individuals’ income, and goods with many substitutes are likely to have highly elastic demand curves. Examples of such goods are private plane rides and sports vehicles.

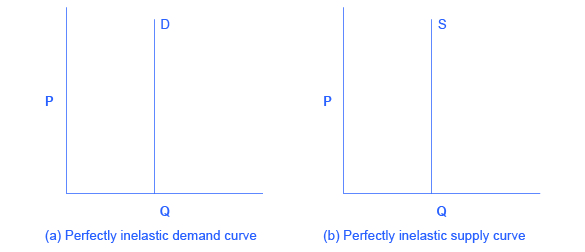
Zero elasticity or perfect inelasticity, as Figure 4.5 depicts, refers to the extreme case in which a percentage change in price, no matter how large, results in zero change in quantity. While a perfectly inelastic supply is an extreme example, goods with limited supply of inputs are likely to feature highly inelastic supply curves. Examples include diamond rings or housing in prime locations such as apartments facing Central Park in New York City. Similarly, while perfectly inelastic demand is an extreme case, necessities with no close substitutes are likely to have highly inelastic demand curves. This is the case of life-saving drugs and gasoline.

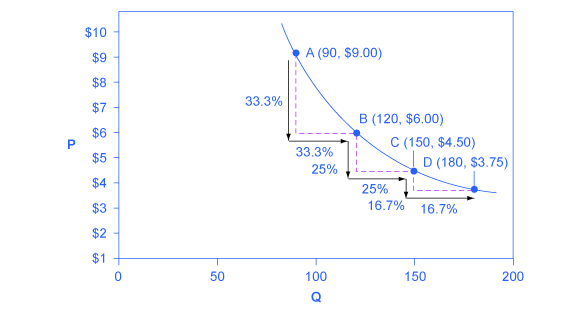
Constant unitary elasticity, in either a supply or demand curve, occurs when a price change of one percent results in a quantity change of one percent. Figure 4.6 shows a demand curve with constant unit elasticity. Constant unitary elasticity, in either a supply or demand curve, occurs when a price change of one percent results in a quantity change of one percent. Figure 4.6 shows a demand curve with constant unit elasticity. Using the midpoint method, you can calculate that between points (A) and (B) on the demand curve, the price changes by 28.6% and quantity demanded also changes by 28.6%. Hence, the elasticity equals 1. Between points (B) and (C), price again changes by 28.6% as does quantity, while between points (C) and (D) the corresponding percentage changes are 22.2% for both price and quantity. In each case, then, the percentage change in price equals the percentage change in quantity, and consequently elasticity equals 1. Notice that in absolute value, the declines in price, as you step down the demand curve, are not identical. Instead, the price falls by $2 from A to B, by a smaller amount of $1.50 from B to C, and by a still smaller amount of $0.90 from C to D. As a result, a demand curve with constant unitary elasticity moves from a steeper slope on the left and a flatter slope on the right—and a curved shape overall. Notice that in absolute value, the declines in price, as you step down the demand curve, are not identical. Instead, the price falls by $23 from A to B, by a smaller amount of $1.50 from B to C, and by a still smaller amount of $.90 from C to D. As a result, a demand curve with constant unitary elasticity has a steeper slope on the left and a flatter slope on the right—and a curved shape overall.

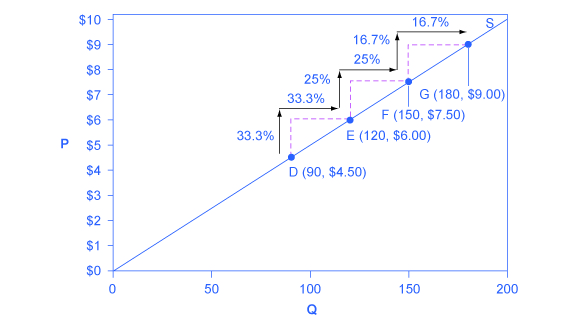
Unlike the demand curve with unitary elasticity, the supply curve with unitary elasticity is represented by a straight line, and that line goes through the origin. In each pair of points on the supply curve there is an equal difference in quantity of 30. However, in percentage value, using the midpoint method, the steps are decreasing as one moves from left to right, from 28.6% to 22.2% to 18.2%, because the quantity points in each percentage calculation are getting increasingly larger, which expands the denominator in the elasticity calculation of the percentage change in quantity.

Consider the price changes moving up the supply curve in Figure 4.7. From points (D) to (E) to (F) and to (G) on the supply curve, each step of $1.50 is the same in absolute value. However, if we measure the price changes in percentage change terms, using the midpoint method, they are also decreasing, from 28.6% to 22.2% to 18.2%, because the original price points in each percentage calculation are getting increasingly larger in value, increasing the denominator in the calculation of the percentage change in price. Along the constant unitary elasticity supply curve, the percentage quantity increases on the horizontal axis exactly match the percentage price increases on the vertical axis—so this supply curve has a constant unitary elasticity at all points.