Decimals

Michelle Manes

54 Decimals

Up to now our “Dots & Boxes” model has consisted of a row of boxes extending infinitely far to the left. Why not have boxes extending to the right as well?

Let’s work specifically with a 1←10 rule and see what boxes to the right could mean.

Notation

It has become convention to separate boxes to the right of the ones place with a decimal point. (At least, this is what the point is called in the base ten world… “dec” means “ten” after all!)

What is the value of the first box to the right of the decimal point? If we denote its value as $x$ , we have that ten $x$ ’s is equivalent to 1. (Remember, we are using a 1 ← 10 rule.)

From $10x = 1$ we get that $x = \frac 1{10}$ .

Call the value of the next box to the right $y$ .

From $10y = \frac 1{10}$ we get $y=\frac 1{100}$ .

If we keep doing this, we see that the boxes to the right of the decimal point represent the reciprocals of the powers of ten.

Example: 0.3

The decimal $0.3$ is represented by the picture:

It represents three groups of $\frac 1{10}$ , that is:

$0.3 = \frac 3{10}.$

Example: 0.007

The decimal $0.007$ is represented by the picture:

It represents seven groups of $\frac 1{1000}$ .

Of course, some decimals represent fractions that can simplify further. For example:

$0.5 = \frac 5{10} = \frac 1 2.$

Similarly, if a fraction can be rewritten to have a denominator that is a power of ten, then it is easy to convert it to a decimal. For example, $\frac 3 5$ is equivalent to $\frac 6{10}$ , and so we have:

$\frac 3 5 = \frac 6{10} = 0.6.$

Example: 12 3/4

Can you write $12\frac 3 4$ as a decimal? Well,

$12\tfrac 3 4 = 12 + \tfrac 3 4.$

We can write the denominator as a power of ten using the key fraction rule:

$\frac 3 4 \cdot \frac{25}{25} = \frac {75}{100}.$

So we see that:

$12 + \tfrac 3 4 = 12 + \tfrac {75}{100} = 12.75.$

Think / Pair / Share

Draw a “Dots & Boxes” picture for each of the following decimals. Then say what fraction each decimal represents:
$0.09, \qquad\qquad 0.003, \qquad\qquad 0.7, \qquad\qquad 0.0000003.$
Draw a “Dots & Boxes” picture for each of the following fractions. Then write the fraction as a decimal:
$\frac 1{1000}, \qquad\qquad \frac 7{100}, \qquad\qquad \frac9{10}.$
What fractions (in simplest terms) do the following decimals represent?
$0.05, \qquad\qquad 0.2, \qquad\qquad 0.8, \qquad\qquad 0.004.$
Use the key fraction rule to write the following fractions as decimals. Do not use a calculator!
$\frac 25, \qquad\qquad \frac 1{25}, \qquad\qquad \frac 1{20}, \qquad\qquad \frac 1{200}, \qquad\qquad \frac 1 {1250}.$
Some people read 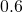$0.6$ out loud as “point six.” Others read it out loud as “six tenths.” Which is more helpful for understanding what the number really is? Why do you think so?

Example: 0.31

Here is a more interesting question: What fraction is represented by the decimal $0.31$ ?

There are two ways to think about this.

Approach 1:

From the picture of the “Dots & Boxes” model we see:

$0.31\ =\ \frac 3{10}+\frac1{100}.$

We can add these fractions by finding a common denominator:

$\frac 3{10}+ \frac 1{100}\ =\ \frac {30}{100} +\frac 1{100}\ =\ \frac {31}{100}.$

So

$0.31 \ = \ \frac{31}{100}.$

Approach 2:

Let’s unexplode the three dots in the $\frac 1{10}$ position to produce an additional 30 dots in the $\frac 1{100}$ position.

So we can see right away that

$0.31 \ = \ \frac{31}{100}.$

On Your Own

Work on the following exercises on your own or with a partner.

1. Brian is having difficulty seeing that $0.47$ represents the fraction $\frac{47}{100}$ . Describe the two approaches you could use to explain this to him.

2. A teacher asked his students to each draw a “Dots & Boxes” picture of the fraction $\frac{319}{1000}$ .

Jin drew this:

Sonia drew this:

The teacher marked both students as correct.

Are each of these solutions correct? Explain your thinking.
Jin said he could get Sonia’s solution by performing some explosions. What did he mean by this? Is he right?

3. Choose the best answer and justify your choice. The decimal $0.23$ equals:

$(a) \ \frac{23}{10} \qquad\qquad (b)\ \frac{23}{100}$

$(c) \ \frac{23}{1,000} \qquad\qquad (d)\ \frac{23}{10,000}.$

4. Choose the best answer and justify your choice. The decimal $0.0409$ equals:

$(a) \ \frac{409}{100} \qquad\qquad (b)\ \frac{409}{1,000}$

$(c) \ \frac{409}{10,000} \qquad\qquad (d)\ \frac{409}{100,000}.$

5. Choose the best answer and justify your choice. The decimal $0.050$ equals:

$(a) \ \frac{50}{100} \qquad\qquad (b) \ \frac{1}{20 }$

$(c) \ \frac{1}{200} \qquad\qquad (d)\ \text{None of these.}$

6. Choose the best answer and justify your choice. The decimal $0.000204$ equals:

$(a)\ \frac{51}{250} \qquad\qquad (b) \ \frac{51}{2500 }$

$(c)\ \frac{ 51}{25000 } \qquad\qquad (d) \ \frac{51}{250000}.$

7. What fraction is represented by each of the following decimals?

$(a) \ 0.567 \qquad\qquad (b) \ 0.031$

$(c) \ 0.4077 \qquad\qquad (d) \ 0.101.$

8. Write each of the following fractions as decimals. Don’t use a calculator!

$(a)\ \frac{73}{100} \qquad\qquad (b) \ \frac{519}{1000}$

$(c) \ \frac{71}{1000} \qquad\qquad (d) \ \frac{7001}{10000}.$

9. Write each of the following fractions as decimals. Don’t use a calculator!

$(a) \ \frac{7}{20} \qquad\qquad (b) \ \frac{16}{25} \qquad\qquad\qquad\quad$

$(c) \ \frac{301}{500} \qquad\qquad (d) \ \frac{17}{50} \qquad\qquad (e) \ \frac{3}{4}.$

10. Write each of the following as a fraction (or mixed number).

$(a) \ 2.3 \qquad\qquad (b) \ 17.04 \qquad\qquad (c) \ 1003.1003$

11. Write each of the following numbers in decimal notation.

$(a) \ 5\frac{3}{10} \qquad\qquad (b) \ 7\frac15 \qquad\qquad (c) \ 13\frac12 \qquad\qquad (d)\ 106\frac3{20}$

$(e) \ \frac{78}{25} \qquad\qquad (f) \ \frac{9}{4} \qquad\qquad (g) \ \frac{131}{40} \qquad\qquad\qquad\qquad$

Think Pair Share

Do $0.19$ and $0.190$ represent the same number or different numbers?

Here are two dots and boxes pictures for the decimal $0.19$ .

And here are two dots and boxes picture for the decimal $0.190$ .

Explain how one “unexplosion” establishes that the first picture of 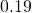$0.19$ is equivalent to the second picture of $0.19$ .

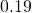Explain how several unexplosions establishes that the first picture of 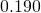$0.190$ is equivalent to the second picture of $0.190$ .

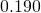Use explosions and unexplosions to show that all four pictures are equivalent to each other.

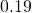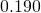So … does $0.19$ represent the same number as $0.190$ ?

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License