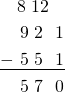Subtraction: Dots and Boxes

Michelle Manes

19 Subtraction: Dots and Boxes

Subtraction as Take-Away

To model addition, we started with two collections of dots (two numbers), and we combined them to form one bigger collection. That’s pretty much the definition of addition: combining two collections of objects. In subtraction, we start with one collection of dots (one number), and we take some dots away.

Example: 376 – 125

Suppose we want to find 376-125 in the dots and boxes model. We start with the representation of 376:

Since we want to “take away” 125, that means:

We take away one dot from the hundreds box, leaving two dots.
We take away two dots from the tens box, leaving five dots.
And we take away five dots from the ones box, leaving one dot.

So the answer is:

$\begin{align*} \phantom{ + } 376 \\ \underline{- 125} \\ \phantom{ + } 251 \end{align*}$

And saying it out the long way we have:

Three hundreds take away one hundred leaves 2 hundreds.
Seven tens take away two tens gives 5 tens.
Six ones take away five ones gives 1 one.

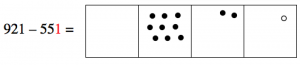
Example: 921 – 551

Let’s try a somewhat harder example: 921-551. We start with the representation of 921:

Since we want to “take away” 551, that means we take away five dots from the hundreds box, leaving four dots.

Now we want to take away five dots from the tens box, but we can’t do it! There are only two dots there. What can we do? Well, we still have some hundreds, so we can “unexplode” a hundreds dot, and put ten dots in the tens box instead. Then we’ll be able to take five of them away, leaving seven.

(Notice that we also have one less dot in the hundreds box; there’s only three dots there now.)

Now we want to take one dot from the ones box, and that leaves no dots there.

So the answer is:

$\begin{align*} \phantom{ + } 921 \\ \underline{- 551} \\ \phantom{ + } 370 \end{align*}$

Think / Pair / Share

Solve the following exercises by thinking about dots and boxes. (You can draw pictures, or just imagine them.)

$\begin{align*} \phantom{ + } 323 && \phantom{ + } 567 && \phantom{ + }389107123\\ \underline{- 148} &&\underline{- 271}&&\underline{- 310462872 }\\ \phantom{ + 323}&& \phantom{ + 271}&& \phantom{ + 389107123}\\ \end{align*}$

Problem 2

Use the dots and boxes technique to solve these problems. Do not covert to base 10! Try to work directly in the base given. It might help to actually draw the pictures.

$\begin{align*} \phantom{ + } 20413_{\text{five}} && \phantom{ + } 6252_{\text{nine}} && \phantom{ + } 4323_{\text{seven}} \\ \underline{- 13244_{\text{five}}} &&\underline{- 4088_{\text{nine}}}&&\underline{- 3524_{\text{seven}}}\\ \phantom{ + 20413_{\text{five}}}&& \phantom{ +4052_{\text{nine}}}&& \phantom{ + 3355_{\text{seven}}}\\ \end{align*}$

The Standard Algorithm for Subtraction

Just like in addition, the standard algorithm for subtraction requires you to work from right to left, and “borrow” (this is really regrouping!) whenever necessary. Notice that in the dots and boxes approach, you don’t need to go in any particular order when you do the subtraction. You just “unexplode” the dots as necessary when computing.

Here’s how the standard algorithm looks with the dots and boxes model for 921 – 551: Start with 921 dots.

Then take away one dot from the ones box.

$\begin{align*} \phantom{ + } 921 \\ \underline{- 551} \\ \phantom{ + } \phantom{55}0 \end{align*}$

Now we want to take away five dots from the tens box. But there aren’t five dots there. So we “unexplode” one of the hundreds dots to get more tens:

In the standard algorithm, we show the unxplosion as a regrouping, subtracting one from the hundreds place of 921 and adding ten to the tens place. So we are rewriting

$9 \mid 2 \mid 1 = 8 \mid 12 \mid 1.$

$\begin{align*} \phantom{ + } 8\ 12\ \phantom{1} \\ \phantom{ +}\cancel{9}\ \cancel{2}\ \ 1 \\ \underline{-\ 5\ 5\ \ 1} \\ \phantom{ + } \phantom{\ 5\ }7\ \ 0 \end{align*}$

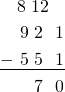
Finally, we want to take away five from the eight dots left in the hundreds column.

$\begin{align*} \phantom{ + } 8\ 12\ \phantom{1} \\ \phantom{ +}\cancel{9}\ \cancel{2}\ \ 1 \\ \underline{-\ 5\ 5\ \ 1} \\ \phantom{ + }\ 5\ 7\ \ 0 \end{align*}$

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License