29 Dividing Fractions: Problems
We’ve spent the last couple of chapters talking about dividing fractions: how to make sense of the operation, how to picture what’s going on, and how to do the computations. But all of this kind of begs the question: When would you ever want to divide fractions, anyway? How does that even come up?
It’s important that teachers are able to come up with situations and problems that model particular operations, which means you have to really understand what the operations mean and when they are used.
Think / Pair / Share
- Use one of our methods (draw a picture, rectangles, common denominator, missing factor) to compute
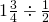 .
. - Come up with a situation where you would want to compute
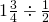 . (That is, write a word problem that would require you to do this computation to solve it.)
. (That is, write a word problem that would require you to do this computation to solve it.)
When to Multiply, When to Divide?
A common answer to
Come up with a situation where you would want to compute
.
Is something like this:
My recipe calls for
cups of flour, but I only want to make half a recipe. How much flour should I use?
But that problem doesn’t ask you to divide fractions. It asks you to cut your recipe in half, which means dividing by 2 or multiplying by ![]() .
.
Why is it so hard to come up with division problems that use fractions? Maybe it’s because fractions are already the answer to a division problem, so you’re dividing and then dividing some more. Maybe it’s because they just make it look so complicated. In any case, it’s worth spending some time thinking about division problems that involve fractions and how to recognize and solve them.
One handy trick: Write a problem that involves division of whole numbers, and then see if you can change the numbers to fractions in a sensible way.
Examples
Here are some division problems involving whole numbers:
- I have 10 feet of ribbon. How many 2-inch pieces can I cut from it?
- I have a fancy old clock that rings once every 15 minutes. How many times will it ring over the course of 2 hours (120 minutes)?
- My fish tank needs 6 gallons of water, and my bucket holds 3 gallons. How many times will I need to fill my bucket in order to fill the tank?
- A recipe calls for 6 cups of flour, and my largest scoop measures exactly 2 cups. How many times should I use it?
- I ran 12 miles and went around the the same route 3 times. How long was the route?
Here are some very similar problems, rewritten to use fractions instead:
- I have
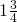 feet of ribbon. How many 6-inch (that’s
feet of ribbon. How many 6-inch (that’s 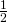 a foot) pieces can I cut from it?
a foot) pieces can I cut from it? - My watch alarm goes off every half hour, and I don’t know how to shut it off. How many times will it go off during the
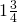 hour movie?
hour movie? - My fish tank needs
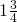 gallons of water, and my bucket holds
gallons of water, and my bucket holds 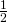 gallon. How many times will I need to fill my bucket in order to fill the tank?
gallon. How many times will I need to fill my bucket in order to fill the tank? - I want to measure
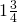 cups of flour for a recipe, but I only have a
cups of flour for a recipe, but I only have a 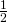 cup measuring cup. How many times should I fill it?
cup measuring cup. How many times should I fill it? - I ran
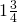 miles before I twisted my ankle. I only finished half the race. How long was the race course?
miles before I twisted my ankle. I only finished half the race. How long was the race course?
For each one of the fraction division questions, we can understand why it’s a division problem:
- I have
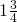 feet of ribbon. How many 6-inch (that’s
feet of ribbon. How many 6-inch (that’s 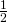 a foot) pieces can I cut from it? This means making equal groups of
a foot) pieces can I cut from it? This means making equal groups of 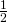 foot each and asking how many groups. That’s quotative division.
foot each and asking how many groups. That’s quotative division. - My watch alarm goes off every half hour, and I don’t know how to shut it off. How many times will it go off during the
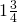 hour movie? Again, we’re making equal groups of
hour movie? Again, we’re making equal groups of 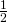 hour each, and asking how many groups. Quotative division.
hour each, and asking how many groups. Quotative division. - My fish tank needs
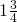 gallons of water, and my bucket holds
gallons of water, and my bucket holds 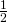 gallon. How many times will I need to fill my bucket in order to fill the tank? Once again: we’re making equal groups of
gallon. How many times will I need to fill my bucket in order to fill the tank? Once again: we’re making equal groups of 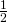 gallon each, and asking how many groups (buckets).
gallon each, and asking how many groups (buckets). - I want to measure
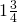 cups of flour for a recipe, but I only have a
cups of flour for a recipe, but I only have a 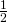 cup measuring cup. How many times should I fill it? This is making equal groups of
cup measuring cup. How many times should I fill it? This is making equal groups of 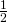 cup and asking how many groups.
cup and asking how many groups. - I ran
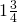 miles before I twisted my ankle. I only finished half the race. How long was the race course? This one is a little different. This one is a little different. It’s the fraction version of partitive division.
miles before I twisted my ankle. I only finished half the race. How long was the race course? This one is a little different. This one is a little different. It’s the fraction version of partitive division.
Recall what partitive division asks: For ![]() , we ask 20 is 4 groups of what size?
, we ask 20 is 4 groups of what size?

So for ![]() , we ask:
, we ask: ![]() is half a group of what size?
is half a group of what size?

Think / Pair / Share
You try it.
- First write five different division word problems that use whole numbers. (Try to write at least a couple each of partitive and quotative division problems.)
- Then change the problems so that they are fraction division problems instead. You might need to rewrite the problem a bit so that it makes sense.
- Solve your problems!
