12 Number Systems
Our number system is a western adaptation of the Hindu-Arabic numeral system developed somewhere between the first and fourth centuries AD. However, numbers have been recorded with tally marks throughout history. The Ishango Bone[1] from Africa is about 25,000 years old. It’s the lower leg bone from a baboon, and contains tally marks. We know the marks were used for counting because they appear in distinct groups.
This reindeer antler[2] from France is about 15,000 years old, and also shows clearly grouped tally marks.
.jpg)
Of course, we still use tally marks today![3]
Base ten numbers (the ones you have probably been using your whole life), and base b numbers (the ones you’ve been learning about in this chapter) are both positional number systems.
Definition
A positional number system is one way of writing numbers. It has unique symbols for 1 through b – 1, where b is the base of the system. Modern positional number systems also include a symbol for 0.
The positional value of each symbol depends on its position in the number:
- The positional value of a symbol in the first position is just its face value.
- The positional value of a symbol in the second position is b times its value.
- The positional value of a symbol in the third position is
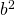times its value. - And so on.
The value of a number is the sum of the positional values of its digits.
Definition
In an additive number system, the value of a written number is the sum of the face values of the symbols that make up the number. The only symbol necessary for an additive number system is a symbol for 1, however many additive number systems contain other symbols.
History: Roman numerals
The ancient Romans used a version of an additive number systems. The Romans represented numbers this way:
| number | Roman Numeral |
| 1 | I |
| 5 | V |
| 10 | X |
| 50 | L |
| 100 | C |
| 500 | D |
| 1,000 | M |
So the number 2013 would be represented as MMXIII. This is read as 2,000 (two M’s), one ten (one X), and three ones (three I’s).
For any additive number system very large numbers become impractical to write. To represent the number one million in Roman numerals it would take one thousand M’s!
However, the Roman numerals did have one efficiency advantage: The order of the symbols mattered. If a symbol to the left was smaller than the symbol to the right, it would be subtracted instead of added. So for example nine is represented as IX rather than VIIII.
Think / Pair / Share
If you don’t already know how to use Roman numerals, research it a little bit. Then answer these questions.
- Write the numbers 1–20 in Roman numerals.
- What is the maximum number of symbols needed to write any number between 1 and 1,000 in Roman Numerals? Justify your answer.
The earliest positional number systems are attributed to the Babylonians (base 60) and the Mayans (base 20). These positional systems were both developed before they had a symbol or a clear concept for zero. Instead of using 0, a blank space was used to indicate skipping a particular place value. This could lead to ambiguity.
Suppose we didn’t have a symbol for 0, and someone wrote the number
![\[2 \ \ 3.\]](https://pressbooks.oer.hawaii.edu/mathforelementaryteachers/wp-content/ql-cache/quicklatex.com-9cf2debb3612955c89da4060d51c992e_l3.png "Rendered by QuickLaTeX.com")
It would be impossible to tell if they mean 23, 203, 2003, or maybe two separate numbers (two and three).
At the time, Roman Numerals dominated Europe, and the official means of calculations was the abacus. Muḥammad ibn Mūsā al-Khwārizmī[5] described the use of Hindu-Arabic system in his book On the Calculation with Hindu Numerals in 825 CE, but it was not well-known in Europe.
Fibonacci’s book Liber Abaci described the Hindu-Arabic system and its business applications for a European readership. His book was well-received throughout Europe, and it marked the beginning of a reawakening of European mathematics.
History: Hawaiian numbers
The Hindu-Arabic number system is now used nearly exclusively throughout the globe. But many cultures had their own number systems before contact and trade with other countries spread the work of al-Khwārizmī throughout the world.
There is evidence that pre-contact Hawaiians actually used two different number systems. Depending on what they were counting, they might use base 4 instead (or a mixed base-10 and base-4 system). One theory is that certain objects (fish, taro, etc.) were often put in bundles of 4, so were more natural to count by 4’s than by 10’s. The number four also had spiritual significance in Hawaiian culture.
 |
Humans have 5 fingers on each hand[6], making base ten a natural choice for counting. But there are 4 gaps between the fingers, meaning that a hand can carry four fish or taro plants or similar objects, making base four a natural choice for some cultures. |
In the mixed base system, instead of powers of 10, numbers are broken down into sums of numbers that look like 4 times a power of 10 (40, 400, 4000, etc.).
| 1 | ‘ekahi |
| 2 | ‘elua |
| 3 | ‘ekolu |
| 4 | ‘ehā (or kauna) |
| 5 | ‘elima |
| 6 | ‘eono |
| 7 | ‘ehiku |
| 8 | ‘ewalu |
| 9 | ‘eiwa |
| 10 | ‘umi |
| 11–19 | ‘umi kumamā {kahi, lua, kolu, hā, etc.} |
| 20 | iwakālua |
| 21–29 | Iwakālua kumamā {kahi, lua, kolu, hā, etc.} |
| 30 | kanakolu |
| 31–39 | kanakolu kumamā {kahi, lua, etc.} |
| 40 | kanahā |
| 400 | lau |
| 4,000 | mano |
| 40,000 | kini |
| 400,000 | lehu |
Here are a few examples (refer to the table above for the Hawaiian names of the numbers):
Example
‘ekolu kini, ‘ewalu lau me ‘ekahi
translates to three 40,000’s, eight 400’s, and one;
3 ⋅ 40000 + 8 ⋅ 400 + 1 = 123201
Example
5207 = 1 ⋅ 4000 + 3 ⋅ 400 + 7
would be ‘ekahi mano, ‘ekolu lau me ‘ehiku
On Your Own
Work on the following exercises on your own or with a partner.
1. Translate this Hawaiian number to English and then write it in base ten.
‘ekahi kanahā me kanakolu kumamāiwa
2. Translate this base‐ten number to Hawaiian.
1,573
Think / Pair / Share
How is learning about different number systems (including representing numbers in different bases) valuable to you as a future teacher?
- Image of Ishango bone by Ben2 (Own work), CC-BY-SA-3.0 or CC BY-SA 2.5-2.0-1.0], via Wikimedia Commons. ↵
- Image of antler By Ryan Somma from Occoquan, USA [CC BY-SA 2.0], via Wikimedia Commons ↵
- Image of Hanakapiai beach warning sign by God of War at the English language Wikipedia [GFDL or CC-BY-SA-3.0], via Wikimedia Commons. ↵
- Image of Fibonacci via Wikimedia Commons, in the public domain. ↵
- Image of al-Khwarizmi statue by M. Tomczak [CC BY-SA 3.0], via Wikimedia Commons. ↵
- Image of hand from https://pixabay.com, licensed under CC0 Creative Commons. ↵
