The following is from http://pvs.kcc.hawaii.edu/ike/hookele/modern_wayfinding.html.

A voyage undertaken using modern wayfinding has three components:

Design a course strategy, which includes a reference course for reaching the vicinity of one’s destination, hopefully upwind, so that the canoe can sail downwind to the destination rather than having to tack into the wind to get there. (Tacking involves sailing back and forth as closely as possible into the wind to make progress against the wind; its very arduous and time-consuming, something to be avoided if at all possible, particularly at the end of a long, difficult voyage.)

During the voyage, holding as closely as possible to the reference course while keeping track of (1) distance and direction traveled; (2) one’s position north and south and east and west of the reference course and (3) the distance and direction to the destination.

Finding land after entering the vicinity of the destination, called a target screen or ‘the box’.

So how is the navigation done — especially component (2) — through thousands of miles of open ocean? You can’t see land. How can you hold closely to the reference course? How can you keep track of distance and direction traveled? How can you even know if you’re going in the right direction if all you can see is blue ocean and blue sky?

By day, the navigators use their deep knowledge of the oceans. Which way do the winds blow? Which way do the prevailing currents move? Clouds in the sky, flotsam in the water, and animal behaviors give them great insight into where land might be, and where they are in relation to it.

By night, they use the stars. In this section, you’ll learn just a tiny fraction of what these master navigators know about the stars.

Star Compass

A fundamental tool for navigators on Hōkūle`a and other voyaging canoes is a star compass. Here’s a picture of Mau Piailug^[2] and a star compass^[3] he used in his teaching.

The object in the center of the circle represents the canoe. The shells along the outside represent directional points. The idea is to imagine the stars rising up from the horizon in the east, traveling through the night sky, and setting past the horizon in the west. They move like they’re on a sphere surrounding the Earth (it’s called the celestial sphere).

How is the star compass used in navigation? There are lots of ways. Here’s a (very!) quick overview:

• The canoe is pictured in the middle of the star compass, with all of the houses around.
• Winds and ocean swells move directly across the star compass from north to south or vice versa.
  • If the swells are coming from `Āina Ko`olau, they will be heading in the direction `Āina Kona. (Look at your star compass and trace out this path.)
  • If the wind is coming from Nālani Malani, it will be heading towards Nālani Ho`olua. (Look at your star compass and trace out this path.)
• Stars stay in their houses, but also in their hemisphere. They do not move across the center of the circle.
• Just like the sun, they rise in the east and set in the west.
  • `A`ā (Sirius) rises in Lā Malanai and sets in Lā Kona. (Look at your star compass and trace out this path.)
  • Hōkūle`a rises in `Āina Ko`olau and sets in `Āina Ho`olua. (Look at your star compass and trace out this path.)

A navigator memorizes the houses of over 200 stars. At sunrise and sunset (when the sun or the stars are rising), the navigator can use the star compass to memorize which way the wind is moving and which way the currents are moving. The navigator can then use that information throughout the day or night to ensure the canoe stays on course.

When teaching navigation while sitting on land, it’s perfectly fine to have a rough sketch or model of the star compass. But if you really have to do the navigation, you need to make a very, very precise star compass.

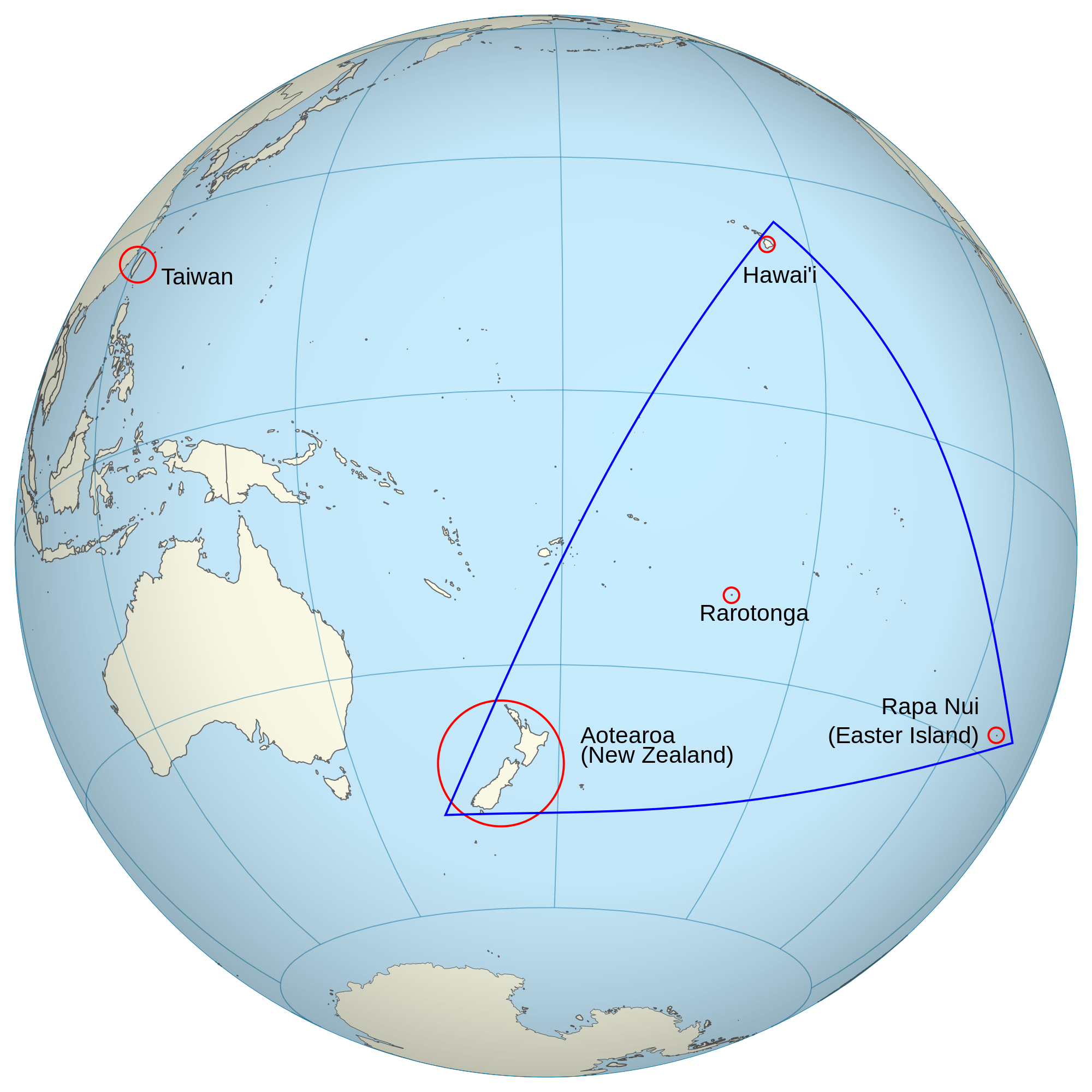
Imagine Nainoa Thompson, who navigated Hōkūle`a on the final leg of her journey from Hawai`i to Rapa Nui, an island even smaller and lower than Ni`ihau. You have to be within 30 miles of Rapa Nui to see it. But a mistake of even one degree would have led to Hōkūle`a being 60 miles off course. And if you end up drifting in the open ocean and supplies run out? Well…

Nainoa Thompson

Of course, a star compass on a piece of paper isn’t so useful when you’re out on a canoe. How do you position it properly? And how do you keep it from getting lost, damaged, or soaking wet? You paint it on the rails of the canoe, permanently!

Look back at the drawing of Hōkūle`a. Find the “kilo” (navigator’s seat) in the rear (aft) of the canoe. There is actually one navigator’s seat on either side of the deck.

The kilo onHōkūle`a[4].	Compass markings on the rails (to be painted more visibly before voyaging)[5].

Nainoa Thompson has said:

Initially, I depended on geometry and analytic mathematics to help me in my quest to navigate the ancient way. However as my ocean time and my time with Mau have grown, I have internalized this knowledge. I rely less on mathematics and come closer and closer to navigating the way the ancients did.

Really he is still doing a lot of mathematics; it’s just mathematics that he has internalized and that is now second nature to him. The ancient navigators may not have spoken of their navigation techniques in the same modern language we’ve been using — compass points and perfect circles and degrees. But their mathematical understanding was truly astonishing.